双向链表

什么是双向链表

双向链表是一种数据结构，由诺干个节点构成，其中每个节点均有三部分构成，分别是前驱接节点，元素，后继节点。双向链表中的节点在内存中是游离状态 {.is-info}

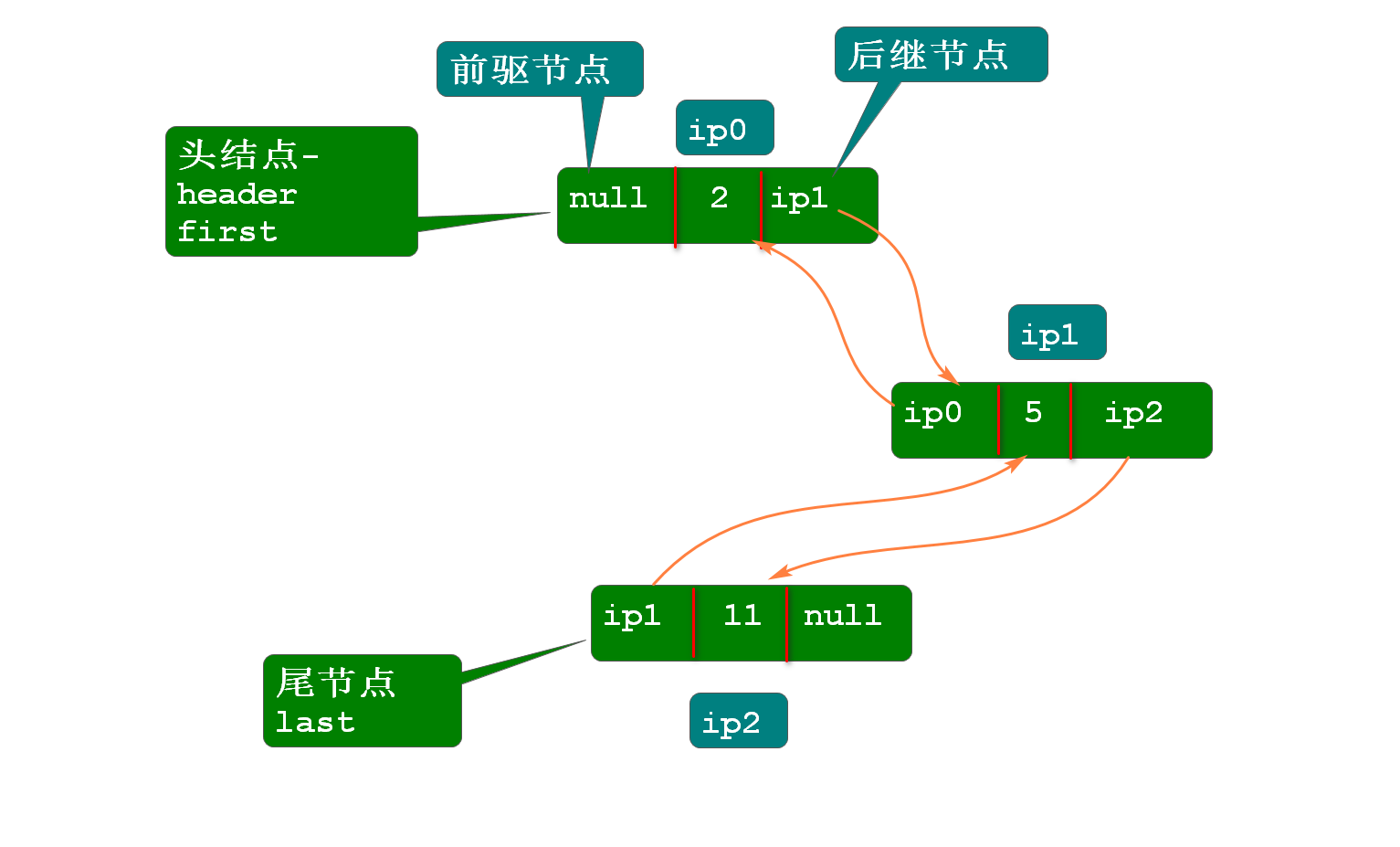
双向链表.png

  • 双向链表的应用：LinkedList

    双向链表中的元素部分保存的都是对象，实际上保存的是元素对象的地址。

对双向链表的操作

  • 添加元素
    • add(E) -- 在链表尾部添加元素 将元素封装到节点中，创建新节点，让新节点和前一个节点建立双向链表的关系。
    • add(int index,E e) -- 在指定位置插入元素 其过程实际上就是断开链，重新构建链的过程
  • 删除元素
    • remove(int index) -- 删除指定位置的元素 其过程实际上依然是断开链，重新构建链的过程
  • 查询元素
    • get(int index) - E 查询方式：对半查找 若查找的位置小于链表长度的一半，则从头节点开始循序查找；否则，从未接地爱你开始逆序查找，这样做可以提高查询效率。

注意点：双向链表中没有下标，index表示的是节点从头开始的顺序位置，indiex并是不双向链表中的属性 {.is-warning}

  • 修改元素
    • set(in index,E e) -- 将新元素替换指定位置的元素

递归

递归是一种思想，应用在边恒中体现为方法调用方法本身。{.is-info}

案例

  • 实现求某个数的阶乘
1! = 1           
2! = 2*1         2*1!
3! = 3*2*1       3*2!
4! = 4*3*2*1     4*3!
5! = 5*4*3*2*1   5*4!
    
    
//f方法用于求出某个数的阶乘   
long f(int n){
   if(n==1)
       return 1;
   return n*f(n-1);
}

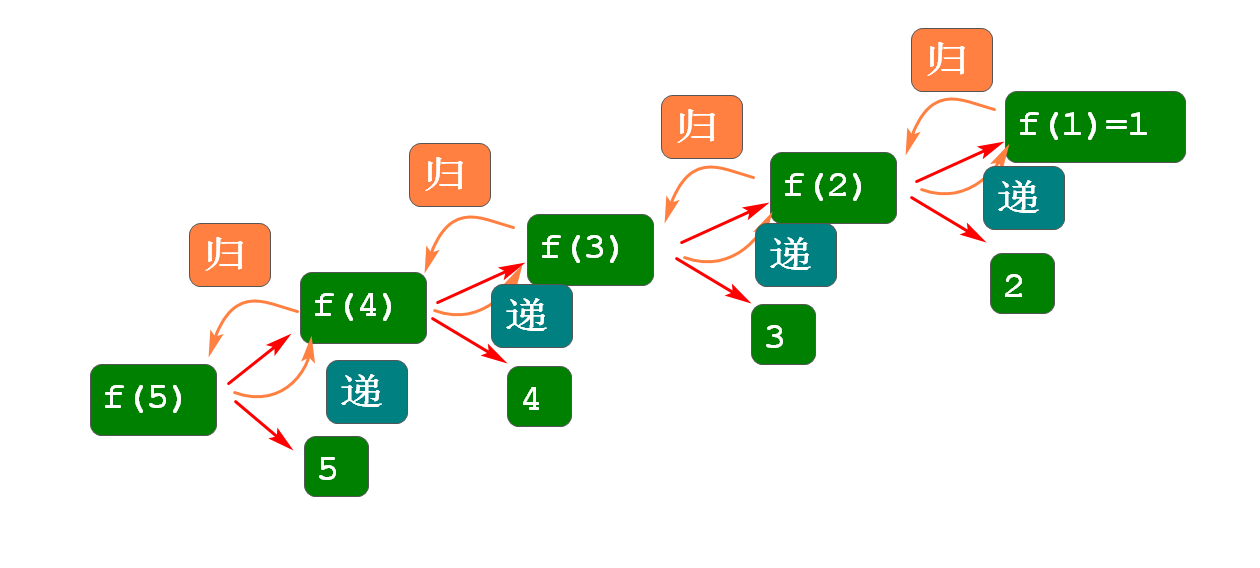
递归.png

  • 斐波那契数列

斐波那契数列（Fibonacci）是这样一组数列：1 1 2 3 5 8 13 21 34 55... 第一位和第二位为1，从第三位开始，每一位的值等于前两位之和{.is-info}

  1. 求出斐波那契数列中第n个位置的值是多少
public static void main(String[] args) {
        System.out.println(f(n));
    }
    
    private static int f(int i) {
        if (i == 1 || i == 2) {
            return 1;
        }
        return f(i - 1) + f(i - 2);
    }
  1. 将斐波那契数列前n个数字输出
public static void main(String[] args) {
        for (int i = 1;i<=n;i++){
            System.out.println(f(i));
        }
    }
    
    private static int f(int i) {
        if (i == 1 || i == 2) {
            return 1;
        }
        return f(i - 1) + f(i - 2);
    }

递归注意点

  1. 递归必须有出口，否则会栈内存溢出（SOF）
  2. 递归是有深度的，若深度太深，可能会造成SOF

栈内存回顾： 用法：当调用某个方式时，会在栈中为这个方法分配属于这个方法的栈帧区域，某个方法的栈帧中保存这个方法中的所有局部变量

树 - tree

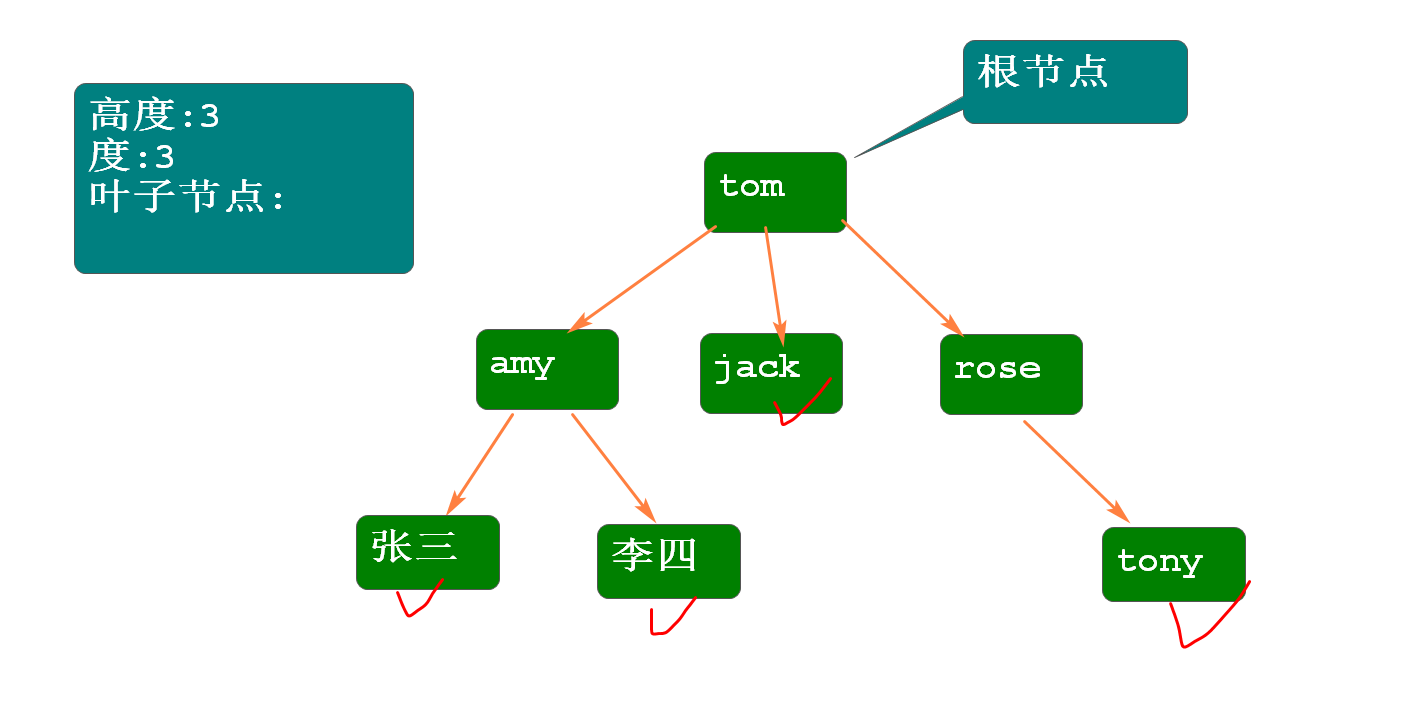
  • 树是数据结构，又若干个节点构成，其中有且仅有一个根节点。
  • 树的术语：
    • 高度：树的层次
    • 根节点：有且仅有一个
    • 度：树种节点的最大子节点数
    • 叶子节点：度为0的节点 树.png

二叉树

  • 度为2的树，则为二叉树

二叉排序树

二叉排序树（Binary Sort Tree）,又称为二叉查找树（Binary Search Tree），亦称二叉搜索树。 是数据结构中的一类。在一般情况下，查询效率比链表结构要高。{.is-info}

  • 特点

    1. 元素不能重复
    2. 左子树中的节点均小于根节点
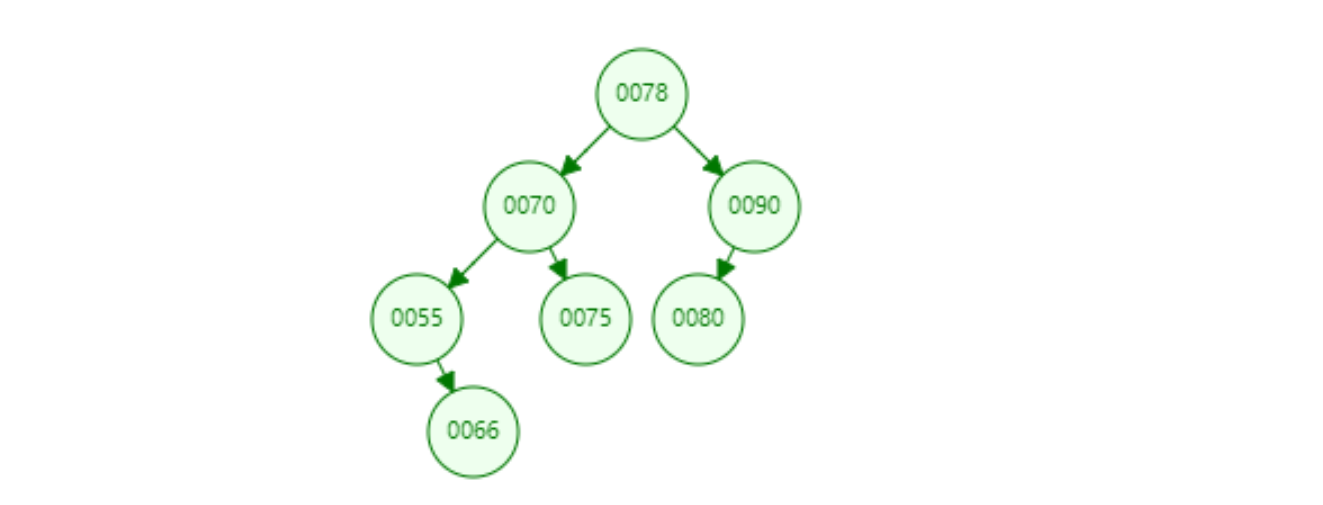
    3. 右子树种的节点均大于根节点 二叉排序树.png

  • 二叉排序树的查询效率高于单向链表 单向链表中，查询元素，最差的情况要查询n次；而在二叉排序树中，每次比较，均可以排除将近一半的数据，所以查询次数会大大减少。

  • 二叉排序树中的元素可以是其他引用类型，但要求改引用类型的对象之间是可比较大小的，如何保证对象之间能比较大小？ 实现Comparable接口，在类中定义比较规则，则对象之间是可比较大小的。

  • 如何保证二叉排序树中的元素是可比较大小的

    • 让元素所属的类实现接口Comparable

    • 比较器：

      Comparable：内比较器，类实现该接口后，需要重写其中的抽象方法，在类的内部定义比较规则
  观察String对象之间的比较
Comparator：外比较器，比较规则定义在类的外部
  通常用于：不改变原有比较规则，要使用新的、临时的比较规则，此时就可以在类的外部实现该接口，定义新的比较规则

定义二叉排序树

public class BinarySearchTree <E extends Comparable<E>> {
    // 根节点
    private Node root;
    
    // 定义内部类表示节点
    private class Node {
        private E ele; // 节点中保存的元素对象
        private Node left; // 左子树指向的节点
        private Node right; // 右子树指向的节点
        
        // 定义有参构造方法，用于创建节点
        Node(E ele) {
            this.ele = ele;
        }
    }
}

  • 添加元素 思路：

    • 判断root是否为null
      • 为null，则将元素封装成节点，成为root，返回true
      • 不为null，和root进行比较，比较的目的是将元素尝试添加为root的left/right子树
        • 和root相等，添加失败，返回false，结束
        • 大于root，尝试添加为root的right，判断right是否为null
          • 为null，则让新元素封装成节点，成为right，添加成功，返回true
          • 不为null，继续喝right的节点进行比较，尝试将元素添加为right的left/right子树
        • 小于，同理

  • 查询元素

    • 判断root是否为null
      • 为null，则树中没有节点，返回null
      • 不为null，以root节点为基准，判断root是否为要找的目标节点
        • 判断e是否和root的ele相等 -- compareTo
          • 若相等，说明root为要找的节点，返回当前节点，结束
          • 若e>ele,则到节点的right去查找目标节点
            • 若right为null，说明目标元素不存在于树中，返回null
            • 若right不为null，判断right纸箱的接地爱你是否为要找的目标节点，重复上述过程
          • 若e<ele,同理

  • 删除元素

    1. 删除叶子节点：让其父节点指向它的引用为null
    2. 删除有一颗子树的节点：让父节点指向它的引用指向删除节点的子节点
    3. 删除有两棵子树的节点：可以选择让删除节点的前驱节点或后继节点上来替换该节点

遍历二叉排序树中的元素

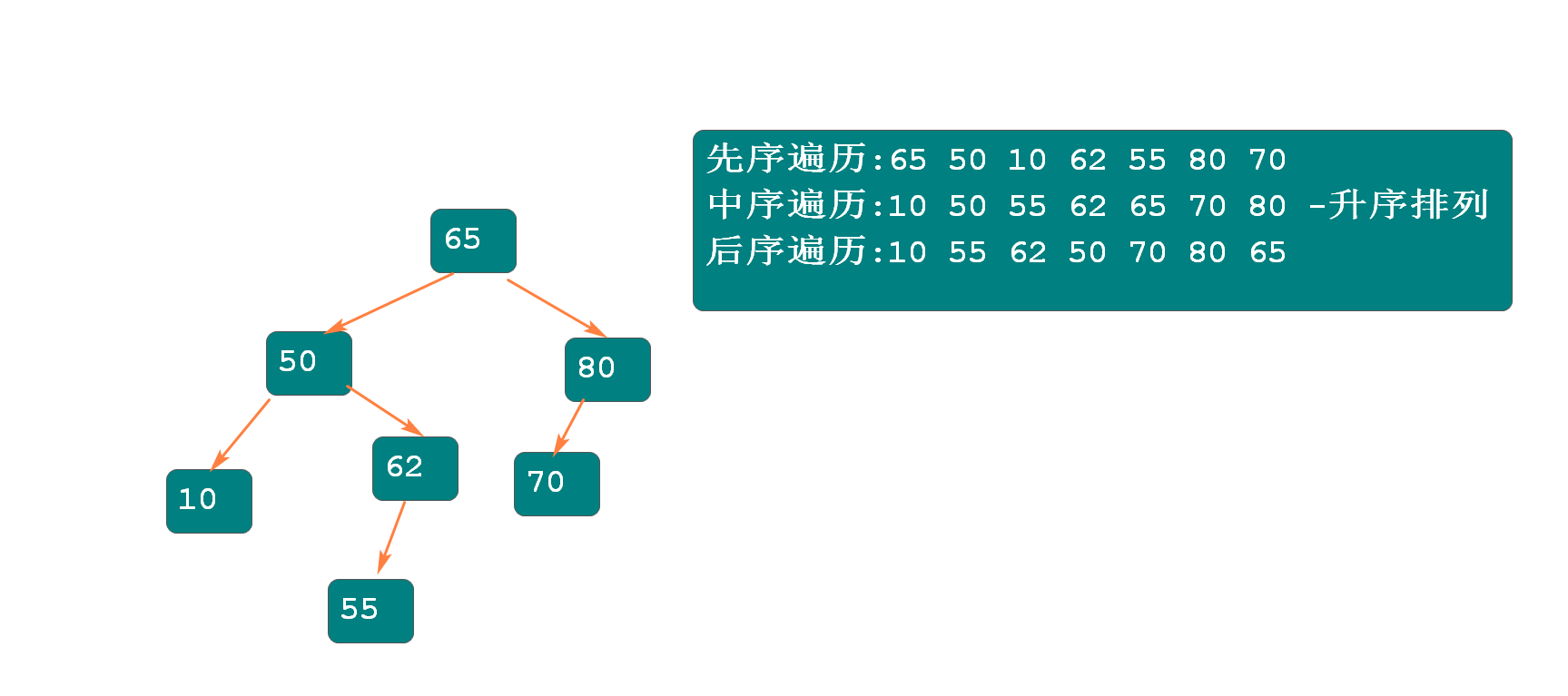
  • 二叉树的遍历：

    • 先序遍历：根 左 右
    • 中序遍历：左 根 右 -- 得到升序排列的结果
    • 后序遍历：左 右 根 遍历二叉树.png

  • 重写toString

目的：实现输出引用，将二叉排序树中的元素遍历，并以以下格式返回： 若树中没有节点，返回[]；若树不为空，则返回[1,2,3,45,78]

  1. 定义方法完成中序遍历，要求该方法返回遍历后元素拼接成的字符串
  2. 重写toString方法，其中调用中序遍历的方法，用于获取所有元素

注意点：非static成员变量属于对象的，会随着对象的重新创建而重新初始化 {.is-warning}

二叉排序树在极端情况下存在的问题

  • 二叉排序树在极端情况下会产生失衡二叉树 失衡二叉树.png
  • 失衡二叉树其实是不希望存在的，因为它失去了二叉排序树的查询优势，现在这种失衡二叉树的查询效率和单向链表一样，此时它就是单向链表
  • 数据结构在设计时已经考虑到了这个问题，所以出现了对二叉排序树的优化，产生了两种新的数据结构。这两种数据结构是基于二叉排序树的，保留了二叉排序树的优势，且避免了缺陷，分别是：
    • AVL树
    • 红黑树

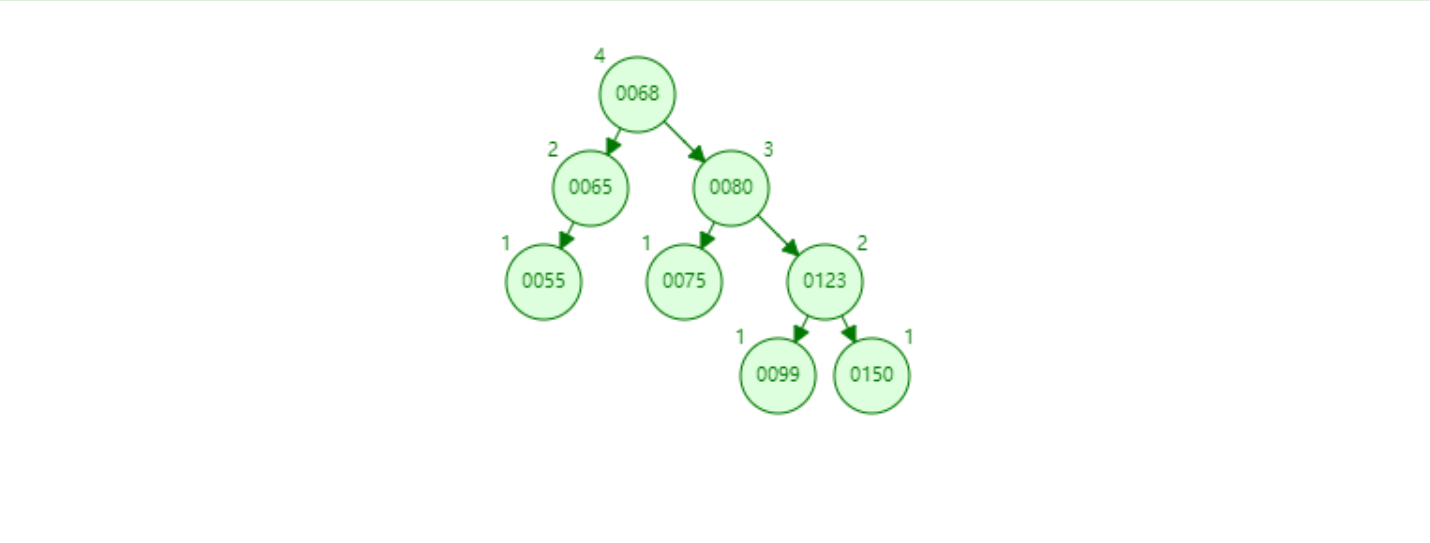
AVL树

平衡二叉树 AVL树通过旋转（左旋、右旋）来保证二叉排序树的平衡状态，AVL树会保证树的左右子树高度差始终是≤1，AVL树达到的平衡状态是绝对平衡（左右字数的高度差≤1） {.is-info}

avl树.png

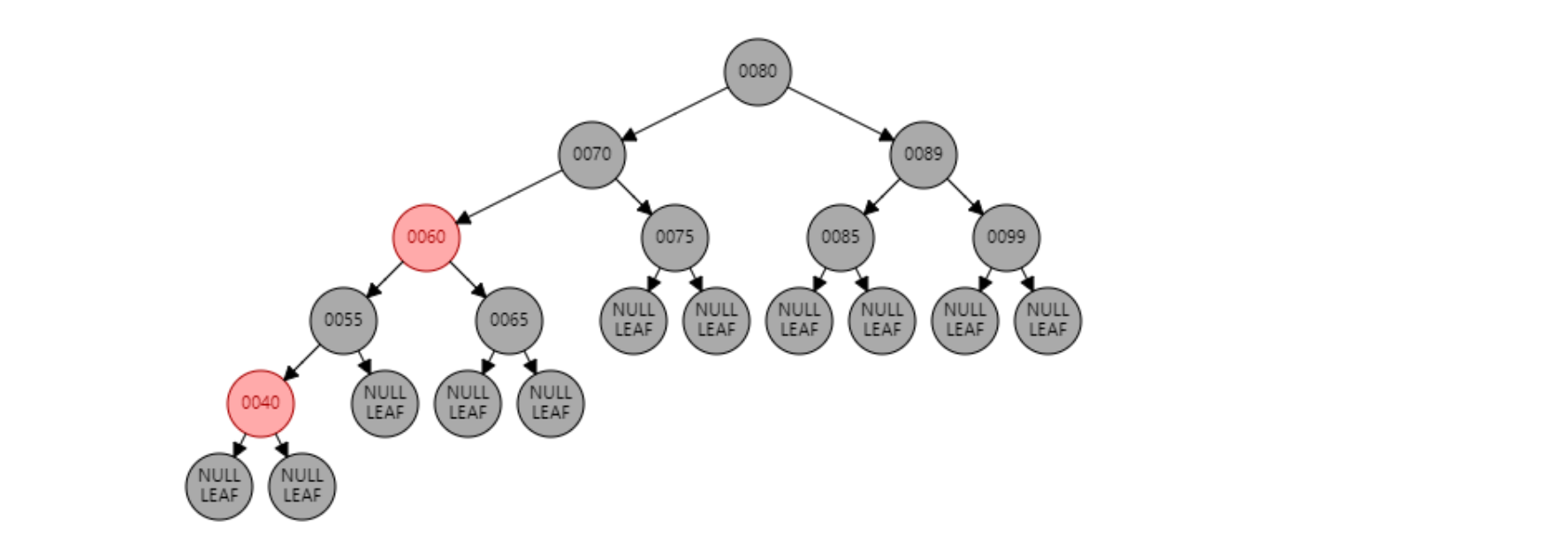
红黑树

红黑树是实现了自平衡的二叉排序树，红黑树达到的是相对平衡状态，而不是绝对平衡状态。 相对平衡状态是指左右子树的高度差可以大于1，红黑树中所有节点的颜色要么是黑色要么是红色{.is-info}

红黑树是怎么实现平衡状态的

通过旋转和调节节点的颜色，两种操作来保证书的平衡状态

红黑树中节点的颜色

有两种节点颜色固定

  • 根节点必然是黑色的
  • 新添加的节点颜色必然是红色的，不过添加成功后，节点的颜色可能被改变

红黑树保证平衡的规则

红黑树是通过旋转（左旋、右旋）和改变节点的颜色来保持树的平衡的 红黑树满足以下5大原则，则认为红黑树达到了平衡状态

  1. 节点是红色或黑色
  2. 根节点是黑色的
  3. 所有叶子节点是黑色（叶子节点是NIL节点）
  4. 每个红色节点的两个子节点都是黑色（从每个叶子到根的所有路径上不能有两个连续的红色节点）
  5. 从任意一个节点到其每个叶子锁经历的简单路径行包含的黑色节点的个数相同 红黑树.png

应用1：TreeMap

TreeMap其实就是红黑树，其实现即为红黑树的视线

  1. 通过debug观察红黑树数据结构
  2. 输出引用，观察toString是如何实现的？ 结果是根据key升序排序的结果，即toString中使用了中序排序

应用2：TreeSet

TreeSet底层调用了TreeMap，其实质为想map中key的那一列保存元素，所以TreeSet也是红黑树的应用

所有的set和map都有这样的关系

  • HashSet -- HashMap 数据结构为散列表，输出引用，得到的结果为无序结果
  • TreeSet -- TreeMap 数据结构为红黑树，输出引用，得到的结果为中序遍历的结果
  • LinkedHashSet -- LinkedHashMap 输出引用，得到的结果为有序结果

散列表

  • 应用类：HashMap

  • 散列表是一种数据结构，这种数据结构的实现：

    • JDK1.8之前，散列表的数据结构为：数组+链表
    • JDK1.8开始，散列表的数据结构为：数组+链表+红黑树 散列表.png

队列

Queue队列：先进先出

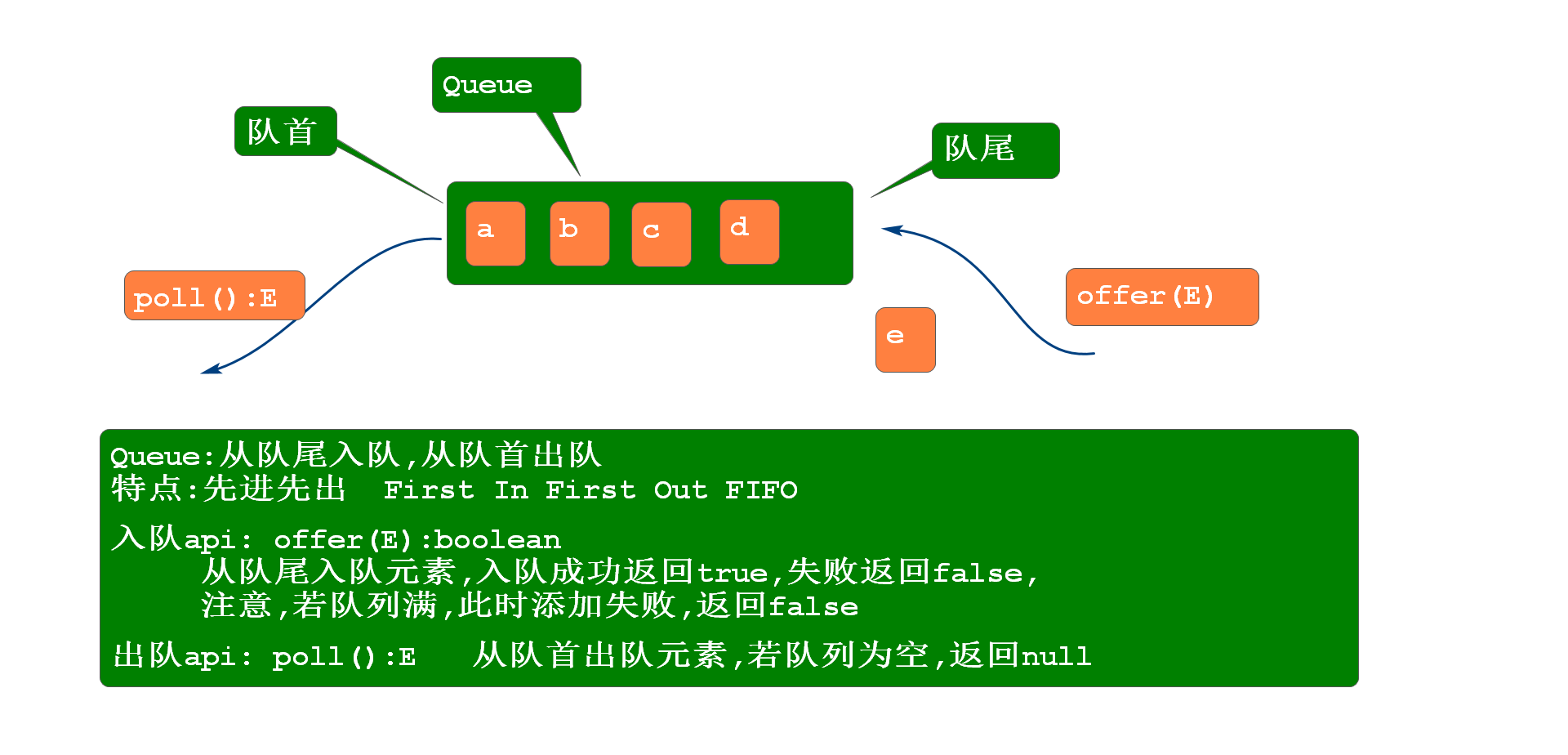
queue.png

  • 入队和出队的API方法
    • boolean offer(E) 入队操作，队列满返回false
    • E poll() 出队操作，队列空返回null
    • E peek() 获取但不从队列中移除元素，队列空返回null

Deque双端队列：两端均可以入队和出队

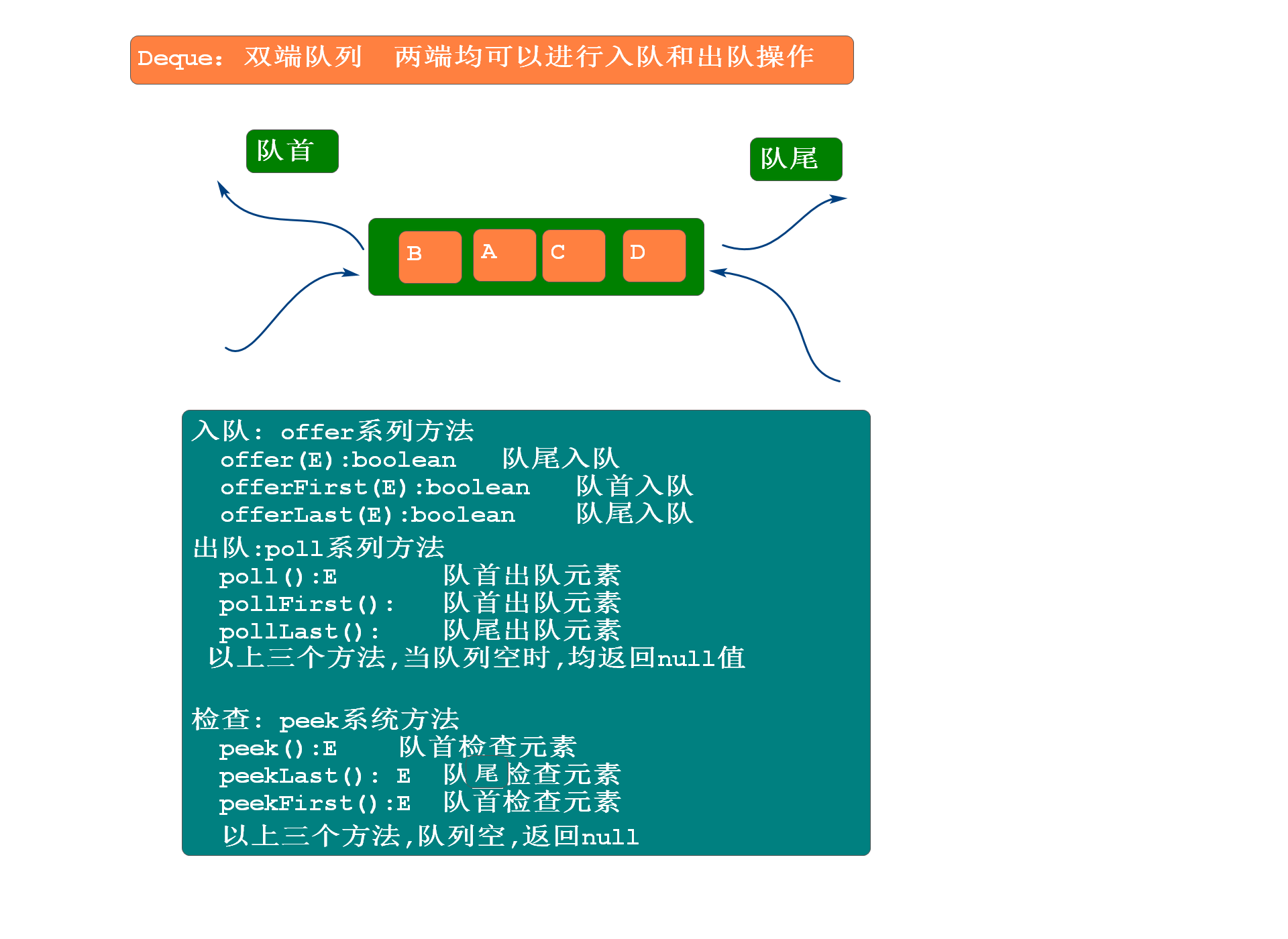
Deque.png

  • API方法
    • 入队：offer系列方法
      • boolean offer(E) 队尾入队
      • boolean offerFirst(E) 队首入队
      • boolean offerLast(E) 队尾入队
    • 出队：poll系列方法
      • E poll() 队首出队元素
      • pollFirst() 队首出队元素
      • pollLast() 队尾出队元素

      注意

      以上三个方法，当队列空时，均返回null

    • 检查：peek系列方法
      • E peek() 队首检查元素
      • E peekFirst() 队首检查元素
      • E peekLast() 队尾检查元素

        注意

        以上三个方法，当队列空时，均返回null

栈：基于双端队列，可以发展出栈结构，其特点为后进先出

栈.png

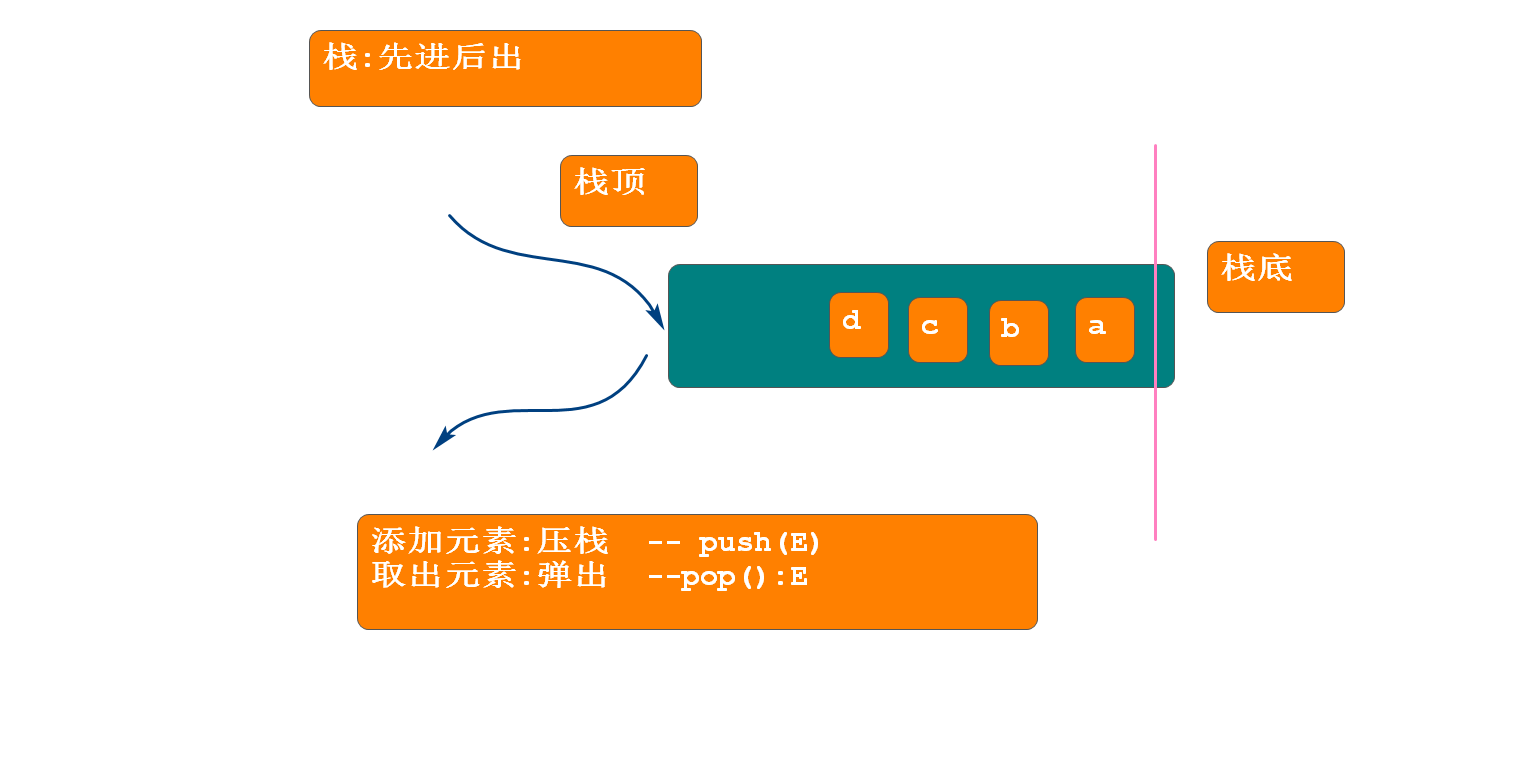
  • API方法
    • push(E) 压栈
    • E pop() 弹出元素