二分查找算法
定义
二分查找算法也称折半查找(Binary Search),它是一种效率较高的查找方法。但是,折半查找要求线性表必须采用顺序存储结构,而且表中元素按关键字有序排列
- 前提要求:
- 线性表必须采用顺序存储结构 -- 数组满足
- 要求元素实现了排序
线性表
线性表是最基本、最简单、也是最常用的一种数据结构。一个线性表是n个具有相同特性的数据元素的有限序列。 线性表中数据元素之间的关系是一对一的关系,即除了第一个和最后一个数据元素之外,其它数据元素都是首尾相接的(注意,这句话只适用大部分线性表,而不是全部。比如,循环链表逻辑层次上也是一种线性表(存储层次上属于链式存储,但是把最后一个数据元素的尾指针指向了首位结点)
顺序存储结构
顺序存储结构是存储结构类型中的一种,该结构是把逻辑上相邻的结点存储在物理位置上相邻的存储单元中,顺序存储结构的主要优点是节省存储空间。结点之间的逻辑关系由存储单元的邻接关系来体现。
查找过程
首先,假设表中元素是按升序排列,将表中间位置记录的关键字与查找关键字比较
如果两者相等,则查找成功;
否则利用中间位置记录将表分成前、后两个子表,
如果中间位置记录的关键字大于查找关键字,则进一步查找前一子表,
否则进一步查找后一子表。
重复以上过程,直到找到满足条件的记录,使查找成功,或直到子表不存在为止,此时查找不成功。

排序算法
冒泡排序
原理机制
相邻元素两两比较,大的(小的)往后排,一轮比较结束后,最大值(最小值)出现在最大下标处,会比较多轮
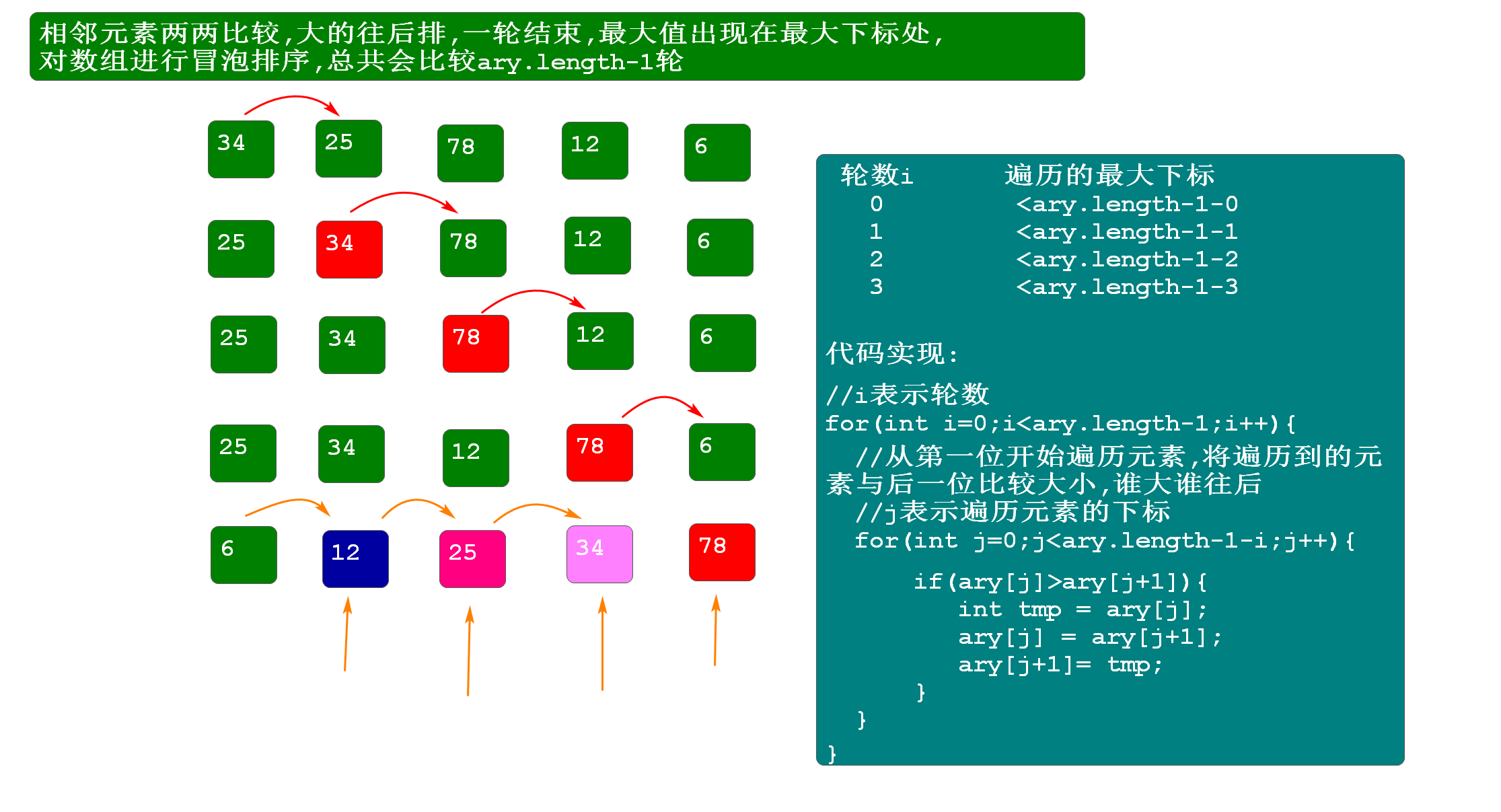
代码实现
class BubbleSort {
public static void main(String[] args) {
int[] ary = {23, 12, 7, 0, 67, 9, 11};
for (int i = 0; i < ary.length - 1; i++) { //i表示轮数
for (int j = 0; j < ary.length - 1 - i; j++) { //j表示遍历元素的下标
if (ary[j] > ary[j + 1]) {
int tmp = ary[j];
ary[j] = ary[j + 1];
ary[j + 1] = tmp;
}
}
}
System.out.println(Arrays.toString(ary));
}
}
选择排序
定义
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理是:第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾。以此类推,直到全部待排序的数据元素的个数为零。选择排序是不稳定的排序方法。
排序规则
- 排序规则解读:从第一位开始,为每一位求应该保存的最小值,除了最后一位
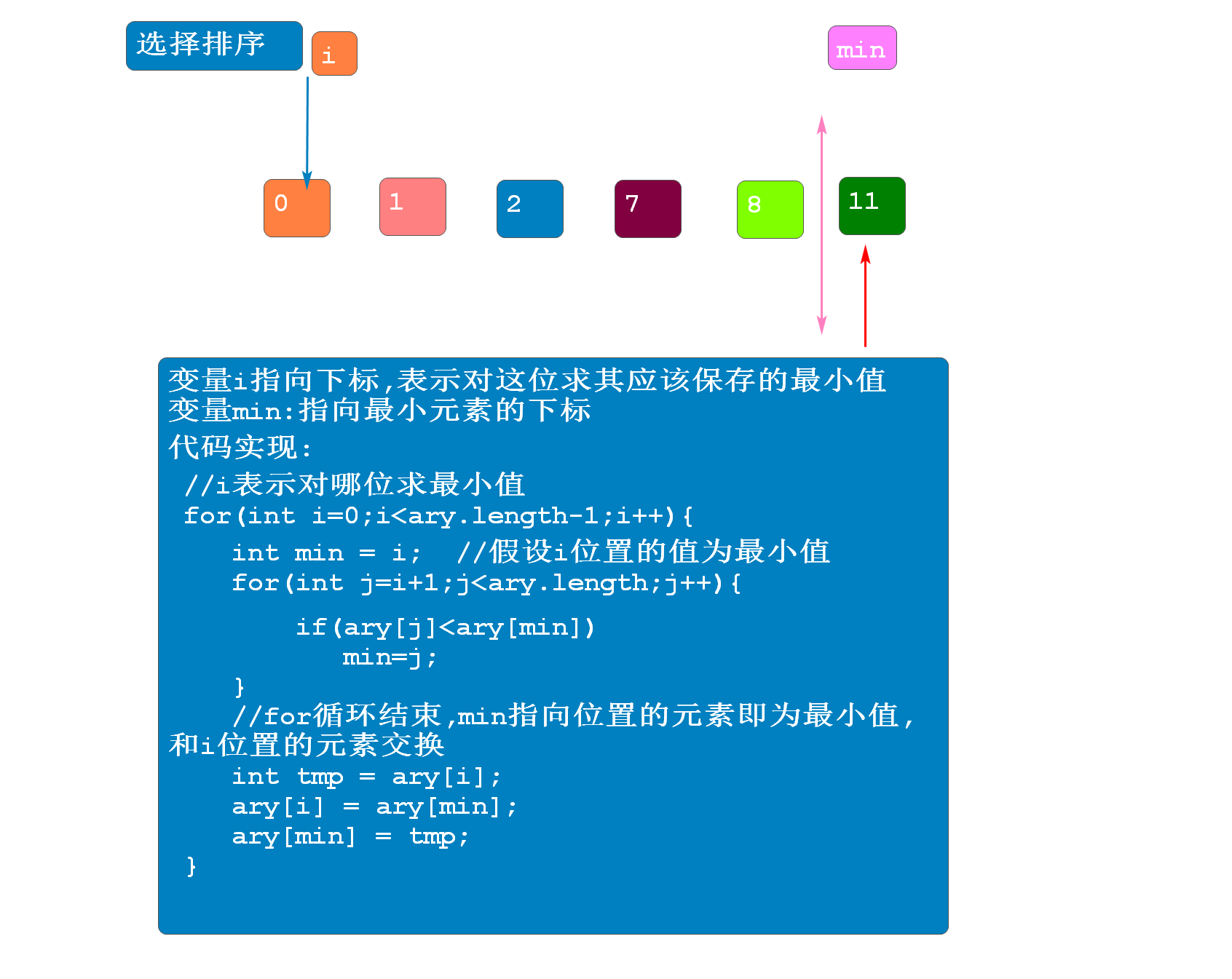
代码实现
class SelectionSort {
public static void main(String[] args) {
for (int i = 0; i < arr.length - 1; i++) {
for (int j = i + 1; j < arr.length; j++) {
if (arr[i] > arr[j]) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
System.out.println(Arrays.toString(arr));
}
System.out.println();
}
}
}
稳定性
提示
选择排序是给每个位置选择当前元素最小的,比如给第一个位置选择最小的,在剩余元素里面给第二个元素选择第二小的,依次类推,直到第n-1个元素,第n个元素不用选择了,因为只剩下它一个最大的元素了。那么,在一趟选择,如果一个元素比当前元素小,而该小的元素又出现在一个和当前元素相等的元素后面,那么交换后稳定性就被破坏了。举个例子,序列5 8 5 2 9,我们知道第一遍选择第1个元素5会和2交换,那么原序列中两个5的相对前后顺序就被破坏了,所以选择排序是一个不稳定的排序算法。
稳定性: 排序后相同元素的相对前后位置是否发生改变;若改变,则该算法是不稳定的;若不改变,则该算法是稳定的.
冒泡排序是稳定的排序算法.
插入排序
定义
插入排序,一般也被称为直接插入排序。对于少量元素的排序,它是一个有效的算法 [1] 。插入排序是一种最简单的排序方法,它的基本思想是将一个记录插入到已经排好序的有序表中,从而一个新的、记录数增1的有序表。
思想
将序列分为排好序部分与未排序部分,对未排序部分的元素进行遍历,将遍历到的元素插入到排好序部分适当的位置去,则排好序部分元素数量增1,直到未排序部分的元素数量为0,则所有元素插入完成,即排序完成.
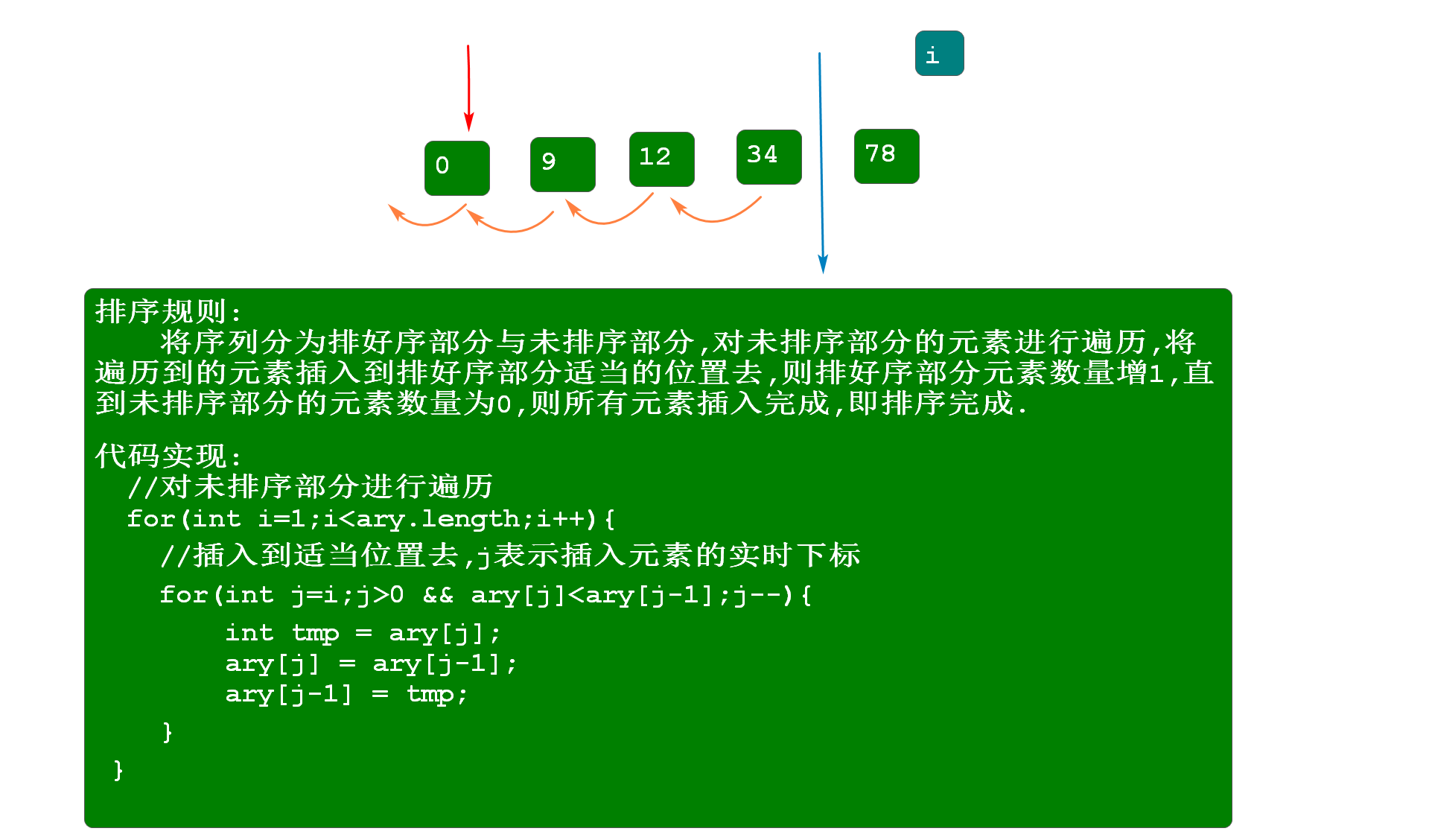
代码实现
class InsertionSort {
public static void main(String[] args) {
for (int i = 0; i < arr.length; i++) {
int j = i;
while (j > 0) {
if (arr[j] < arr[j - 1]) {
int tmp = arr[j];
arr[j] = arr[j - 1];
arr[j - 1] = tmp;
j--;
System.out.println(Arrays.toString(arr));
} else {
break;
}
}
System.out.println();
}
}
}
三种算法排序效率
数组容量相同情况下对比
数组容量为50000
- 冒泡排序:3693毫秒
- 选择排序:1106毫秒
- 插入排序:366毫秒
数组容量为100000
- 冒泡排序:14995毫秒
- 选择排序:4138毫秒
- 插入排序:1470毫秒
数组容量为200000
- 冒泡排序:60749毫秒
- 选择排序:16143毫秒
- 插入排序:5823毫秒
希尔排序
概念
希尔排序(Shell sort)的名称源自于它的发明者Donald Shell。
它通过相距一定间隔的元素来工作,各轮对比所有的距离随着算法的进行而减小,走到只比较相邻元素的最后一轮为止,所以,它也叫做缩减增量排序(Diminishing increment sort)。
从某种程度来看,它是插入排序的升级版。
原理
- 假设有这样一个数组:
int[] arr = {8,1,4,9,0,3,5,2,7,6} - 默认的增量是length/2,本例中数组长度是10,则默认的增量是5,那么,第一个元素将于第6个元素进行对比,其他个元素以此类推
- 希尔排序并不要求增量的大小,除以2的做法是惯例
- 以升序为例,如果左侧的“同组”数据较小,则需要换位,结果将是这样的
{3,1,2,7,0,8,5,4,9,6}(较小的在左侧,较大的在右侧,整个数组依然是无序的) - 第1轮对比完成后,接下来将增量在原基础的基础上除以2,所以新的增量是5/2=2,即第1个和第3个、第5个、第7个、第9个成组对比,以此类推
对着两组元素进行插入排序(代码实现时,每一次的换位都是插入排序,所以,前一次的换位也是通过插入排序实现的),使得这两个部分各自是有序的:{0,1,2,4,3,6,5,7,9,8}
- 接下来这一轮的增量是前次增量除以2,即2/2=1,即全部参与排序
- 对于局部有序的数组,插入裴谞的效率很高,即使全部排序,也非常快
- 当增量大于0室进行每一轮循环,由于上一轮的增量已经是1,而1/2=0,所以终止循环,排序结束。
特殊情况
如果根据增量确定需要对比的关系后,各组对应关系的数量不统一怎么办?
- 通常是数组右侧的若干个元素
- 希尔排序的“排序”过程一般是插入排序,它会先跳过增量值对应数量的元素,然后向右移动,并每次对比“当前下标-增量值”对应的下标元素。
实现步骤分析
在增量值大于0之前进行多轮循环
class ShellSort { public static void main(String[] args) { // 创建需要排序的数组对象 int[] arr = {8, 1, 4, 9, 0, 3, 5, 2, 7, 6}; // 多轮循环 // 初始条件:增量(gap)值为数组长度除以2 // 循环条件:增量>0 // 条件自变:增量除以2 for (int gap = arr.length / 2; gap > 0; gap /= 2) { } } }从与增量值大小相等的下标位置开始,向右循环
class ShellSort { public static void main(String[] args) { // 创建需要排序的数组对象 int[] arr = {8, 1, 4, 9, 0, 3, 5, 2, 7, 6}; // 多轮循环 for (int gap = arr.length / 2; gap > 0; gap /= 2) { // 从与增量值大小相等的下标位置开始,向右循环 for(int i = gap; i < arr.length; i++) { } } } }由于循环后,左侧的“同组”元素可能有多个,人需要使用新的循环来处理
class ShellSort { public static void main(String[] args) { // 创建需要排序的数组对象 int[] arr = {8, 1, 4, 9, 0, 3, 5, 2, 7, 6}; // 多轮循环 for (int gap = arr.length / 2; gap > 0; gap /= 2) { // 准备判断大小及必要的换位,初始下标与增量值相等 for(int i = gap; i < arr.length; i++) { // 接下来的循环表示向左找“同组”的元素尝试对比及必要的换位 // j:左侧“同组”元素的下标,即被对比元素的下标,因为可能有多个,所以需要循环 for(int j = i - gap; j >= 0; j++) { // 内部代码待定 } } } } }处理对比
class ShellSort { public static void main(String[] args) { // 在以上的第3个循环内部 // 判断需对比的两个元素的大小,进行必要的换位 // 注意:使用的下标分别是 j 和 j+gap,后者是因为 j 的值变化时需要跟随调整 if (arr[j] > arr[j + gap]) { // 执行换位,此处省略换位代码 } else { // 注意:此处必须添加break语句 // 基于插入排序的特点,一但左侧元素更小,那么,更左侧的元素肯定也是更小的 // 则,没有必要继续循环下去 break; } } }
代码实现
public class ShellSort {
public static void main(String[] args) {
int[] arr = {8, 1, 4, 9, 0, 3, 5, 2, 7, 6};
System.out.println(Arrays.toString(arr));
System.out.println();
for (int gap = arr.length / 2; gap > 0; gap /= 2) {
for (int i = gap; i < arr.length; i++) {
for (int j = i - gap; j >= 0; j -= gap) {
if (arr[j] > arr[j + gap]) {
int temp = arr[j];
arr[j] = arr[j + gap];
arr[j + gap] = temp;
// 输出数组,观察每次交换后的数组
System.out.println(Arrays.toString(arr));
} else {
break;
}
}
}
System.out.println();
}
}
}
归并排序
概念
- 归并排序是由现代计算机之父——冯·诺依曼提出的算法
- 归并排序的执行效率甚至高于希尔排序
原理
归并排序的核心思想是将2个未排序的“小”数组的所有元素有序的填充到一个新的数组中去,排序的同时形成“合并”。
- 先将两个数组的第一个元素进行对比,将较小的数字(升序排列)填充到新数组中。
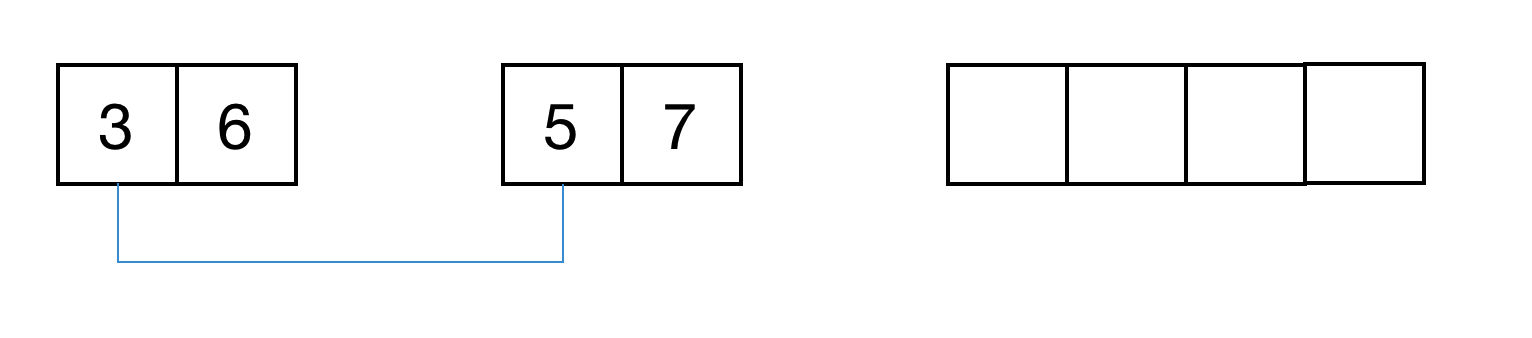
- 将取走数据的数组的下一位,与未被取走数据的数组的那一位对比。
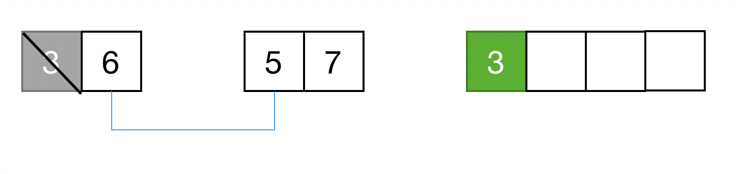
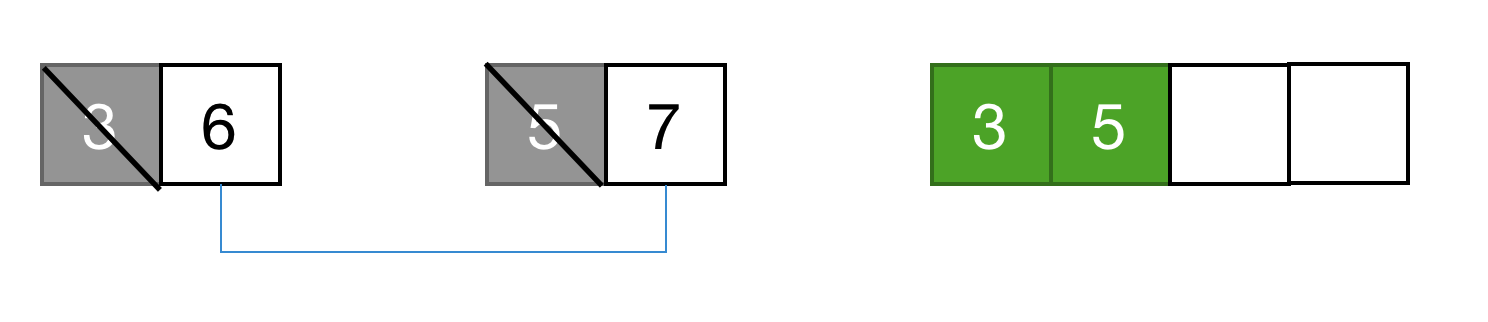
- 继续相同的操作即可······
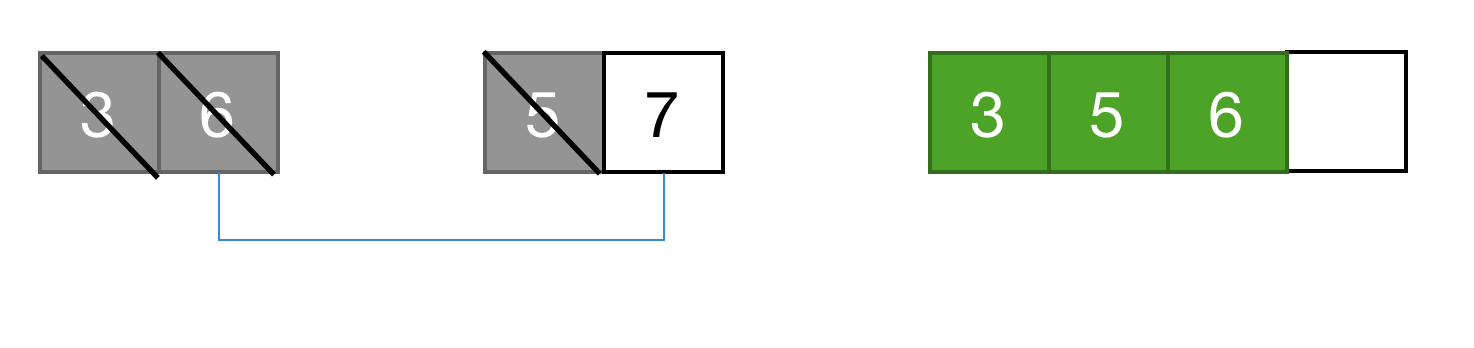
- 直到将最后一个放进去

- 先将两个数组的第一个元素进行对比,将较小的数字(升序排列)填充到新数组中。
以上演示了两个很小的数组的合并过程,事实上,在实际应用中执行排序时,需要排序的原数组只有一个,并且长度通常超过2,那么就需要先将大数组进行反复拆分,得到如同以上演示的小数组(实际执行时,会拆至数组长度为1),再进行排序合并操作,这是一种经典的分治(divide and conquer)策略。
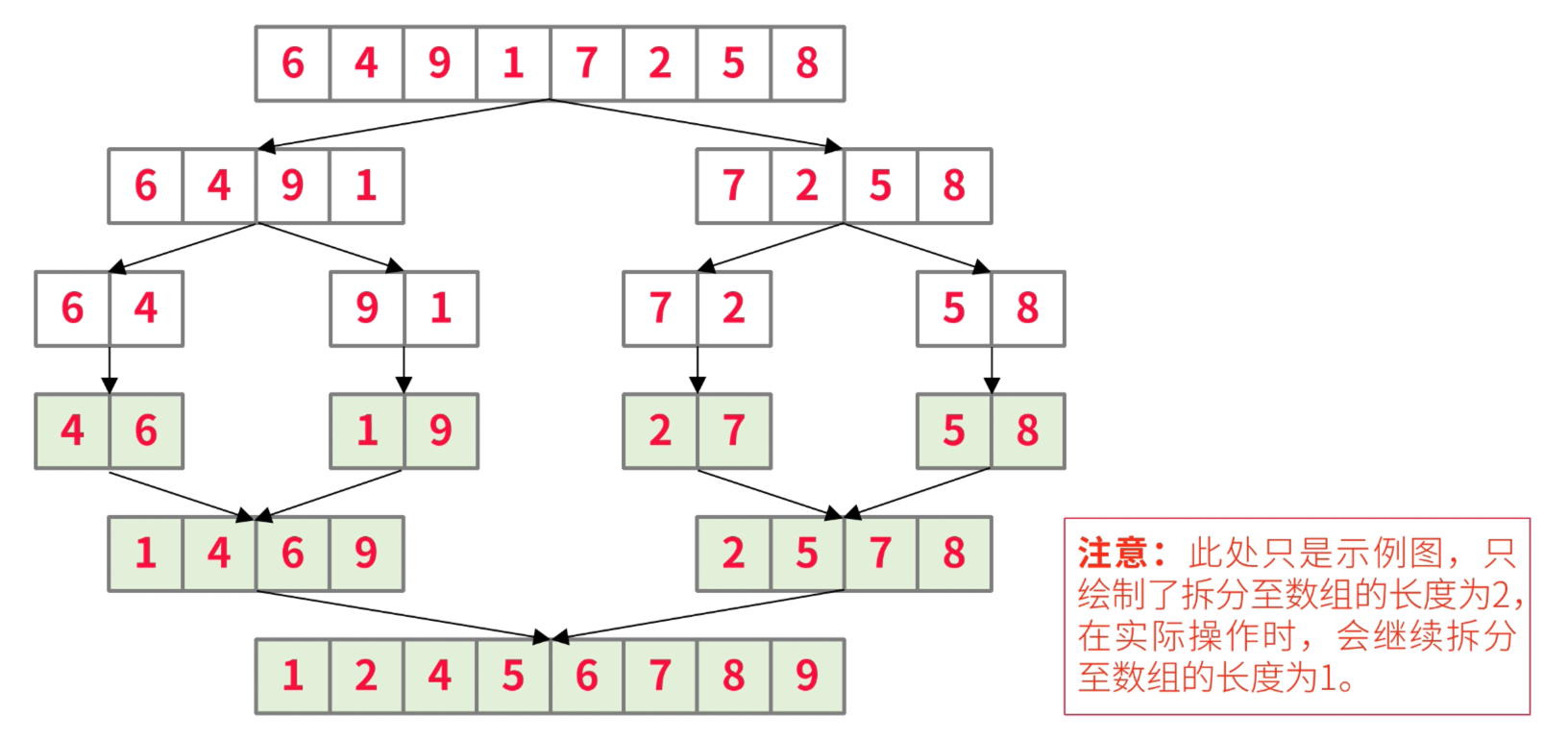
分治策略
分治策略是一种非常经典的思想,它将问题分(divide)成一些小问题,然后递归求解,而治(conquer)的阶段会将分的阶段得到的问题解合并在一起。
- 递归:表现在方法的内部,调用当前方法自身
- 例如在a()方法的内部调用a()方法
- 仅当内部调用的a()方法运行结束,才会继续运行外部a()方法剩余的代码
- 递归:表现在方法的内部,调用当前方法自身
实现步骤分析
- 代码要解决的核心问题是:
- 如何将原数组反复拆分,得到诺干个小数组;
- 如何将两两的小数组合并成较大的数组,直到与原数组相同长度的数组。
分析:将数组一分为二
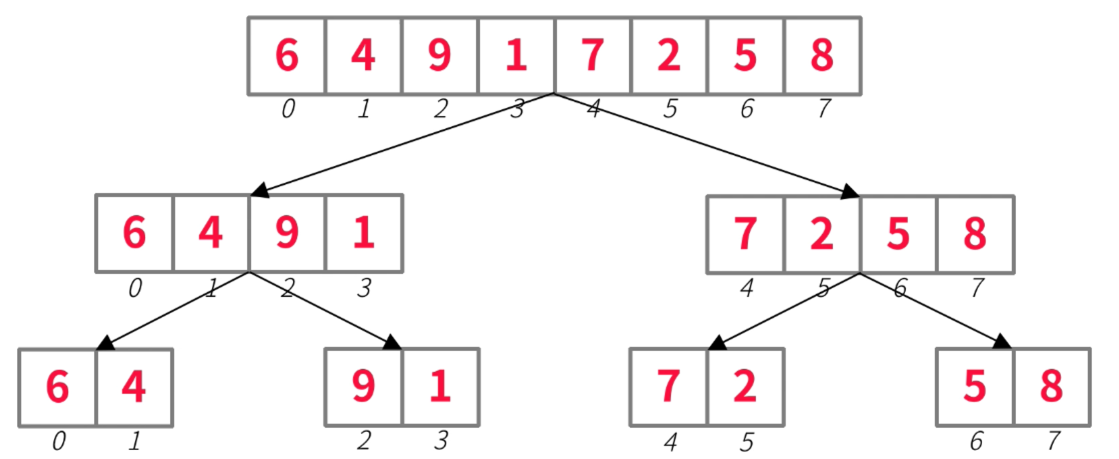
- 中间点:上级数组第1个下标+(上级数组最大下标-上级数组第1个下标)/2
- 左侧:上级数组第1个下标 ~ 中间点
- 右侧:中间点+1 ~ 上级数组最大下标
class Demo{ /** * 这是一个自定义的方法,方法的生命可以参考main()方法 * @param arr 原数组 * @param start 需要被拆分的区间的起始元素下标 * @param end 需要被拆分的区间的结束元素下标 */ public static void mergeSort(int[] arr, int start, int end){ // 求数组需要被拆分的区间的中间点 int mid = start + (end - start) / 2; // 创建两个新的数组,因为每次拆分都执行这个分发,所以得到的左右新数组待定 int[] leftArr = ???; int[] rightArr = ???; } }递归拆分数组
class Demo{ // 注意:方法的返回值将由void改为int[] public static void mergeSort(int[] arr, int start, int end){ // 求数组需要被炒粉的区间的中间点 int mid = start + (end - start) / 2; // 递归:使用当前数组作为参数,继续调用当前方法,也就是按照当前代码继续拆分数组 int[] leftArr = mergeSort(arr, start, end); int[] rightArr = mergeSort(arr, mid + 1, end); // 假设原数组长度为8,调用当前方法时,传入的参数应该为:start=0;end=7 // mergeSort()第1次执行时,mid = 0+(7-0)/2,结果为3 // 为leftArr赋值时发生递归,传入的start=0,mid(end)=3 // 第1次递归时,mid=0+(3-0)/2,结果为1 // 为leftArr赋值时再次发生递归,传入的start=0,mid(end)=1 // 再次递归时,mid=0+(1-0)/2,结果为0 // 为leftArr复制时再次发生递归,传入的start=0,mid(end)=0 // 则leftArr不应该继续拆分 // 为rightArr赋值时同理 } }为了防止递归“死循环”
class Demo{ public static int[] mergeSort(int[] arr, int start, int end) { // 为防止递归出现“死循环”,当end与start相同时(发生在尝试对长度为1的数组再拆分),不必再执行 if (end == start) { // 使用return返回当前片段数组 return new int[]{arr[start]}; } // 求数组长度的中间值,用于将一个数组拆分为两个 int mid = start + (end - start) / 2; // 递归:使用当前数据作为参数,继续调用当前方法 int[] leftArr = mergeSort(arr, start, mid); int[] rightArr = mergeSort(arr, mid + 1, end); } }将两个小数组合并为有序的大数组
假设leftArr和rightArr的长度都是1
class Demo{ public static int[] mergeSort(int[] arr, int start, int end) { // 暂时忽略前序的“拆分数组”的代码,假设leftArr和rightArr已经可用 // 创建新的数组,用于存放合并后的有序结果 int[] newArr = new int[leftArr.length+rightArr.length]; // --- 假设leftArr和rightArr的长度都是1 --- // 将较小的数字放在新数组下标为0的位置,将较大的数字放在新数组下标为1的位置 if (leftArr[0] < rightArr[0]){ newArr[0] = leftArr[0]; newArr[1] = rightArr[0]; }else { newArr[0] = rightArr[0]; newArr[1] = leftArr[0]; } } }处理leftArr和rightArr的长度都大于1的情况,并使用后置自增
class Demo{ public static int[] mergeSort(int[] arr, int start, int end) { // 暂时忽略前序的“拆分数组”的代码,假设leftArr和rightArr已经可用 // 创建新的数组,用于存放合并后的有序结果 int[] newArr = new int[leftArr.length+rightArr.length]; // 声明变量,l,r,n分表表示leftArr,rightArr,newArr的下标变量 int l = 0, r = 0, n = 0; // 当leftArr和rightArr都没有遍历结束之前,一直循环 while (l < leftArr.length && r < rightArr.length) { // 对比两个数组中的元素 if (leftArr[l] <= rightArr[r]) { // 将较小的数字存入到新数组中,并自增较小的数组和新数组的下标变量 newArr[n++] = leftArr[l++]; } else { newArr[n++] = rightArr[r++]; } } } }- 使用“三元表达式”替换if语句
class Demo{ public static int[] mergeSort(int[] arr, int start, int end) { // 暂时忽略前序的“拆分数组”的代码,假设leftArr和rightArr已经可用 // 创建新的数组,用于存放合并后的有序结果 int[] newArr = new int[leftArr.length+rightArr.length]; // 声明变量,l,r,n分表表示leftArr,rightArr,newArr的下标变量 int l = 0, r = 0, n = 0; // 当leftArr和rightArr都没有遍历结束之前,一直循环 while (l < leftArr.length && r < rightArr.length) { // 将较小的数字存入到新数组中,并自增较小的数组和新数组的下标变量 newArr[n++] = leftArr[l] <= rightArr[r] ? leftArr[l++] : rightArr[r++]; } } }
- 使用“三元表达式”替换if语句
合并时,有可能左侧或者右侧其中一侧提前全部合并到新数组,但另一个还有剩余,则将剩余所有数据直接填充到新数组中即可
class Demo{ public static int[] mergeSort(int[] arr, int start, int end) { // 假设此前的循环已经执行结束 // 如果左侧还有剩余,可直接一次全部填充到新数组中 while (l<leftArr.length){ newArr[n++] = leftArr[l++]; } // 如果右侧还有剩余,可直接一次全部填充到新数组中 while (r< rightArr.length){ newArr[n++] = rightArr[r++]; } // 返回新数组 return newArr; } }
代码实现
public class MergeSort {
public static void main(String[] args) {
int[] arr = {8, 1, 4, 9, 0, 3, 5, 2, 7, 6};
System.out.println(Arrays.toString(arr));
System.out.println();
// 调用mergeSort()方法进行排序,并输出最后结果数组
System.out.println(Arrays.toString(mergeSort(arr, 0, arr.length - 1)));
}
/**
* 这是一个已定义的方法,方法的声明可以参考main()方法
*
* @param array 原数组
* @param start 需要被拆分的区间的起始元素下标
* @param end 需要被拆分的区间的结束元素下标
* @return 合并的数组
*/
public static int[] mergeSort(int[] array, int start, int end) {
// 为防止递归出现“死循环”,当end与start相同时(发生在对长度为1的数组再拆分),不必再执行
if (end == start) {
return new int[]{array[start]};
}
// 求数组需要被拆分的区间中中间点
int mid = start + (end - start) / 2;
// 创建两个新的数组,分别表示拆分之后的左侧区域和右侧区域
int[] leftArray = mergeSort(array, start, mid);
int[] rightArray = mergeSort(array, mid + 1, end);
// 创建新的数组,用于存放合并后的有序结果
int[] newArray = new int[leftArray.length + rightArray.length];
// 声明变量,l,r,n分别表示leftArray,rightArray,newArray的下标变量
int l = 0, r = 0, n = 0;
// 当leftArray,rightArray都没有遍历结束之前,一直循环
while (l < leftArray.length && r < rightArray.length) {
// 将较小的数字存入到新数组中,并自增较小的数组和新数组的下标变量
newArray[n++] = leftArray[l] <= rightArray[r] ? leftArray[l++] : rightArray[r++];
}
// 如果左侧还有剩余,可直接一次全部填充到新数组中
while (l < leftArray.length) {
newArray[n++] = leftArray[l++];
}
// 如果右侧还有剩余,可直接一次全部填充到新数组中
while (r < rightArray.length) {
newArray[n++] = rightArray[r++];
}
// 返回新数组
return newArray;
}
}
快速排序
概念
快速排序是目前经典内部排序算法中平均性能最优的算法,通常情况下,它的排序效率明显高于前面五种排序算法。
原理
- 先挑选数组中的某个元素,它将作为所有元素排列大小的分界值
- 作为分界值的数组元素称之为:枢纽元(pivot),也可称之为:主元
- 需要将比枢纽元小的元素放在其左侧位置,将比枢纽元大的元素放在其右侧位置
- 并不关心起左侧区域或右侧区域内的各元素是否有序
以一个数组为例:

- 可以使用最右侧的6最为枢纽元,如需升序排列,则需要先达到以下效果:
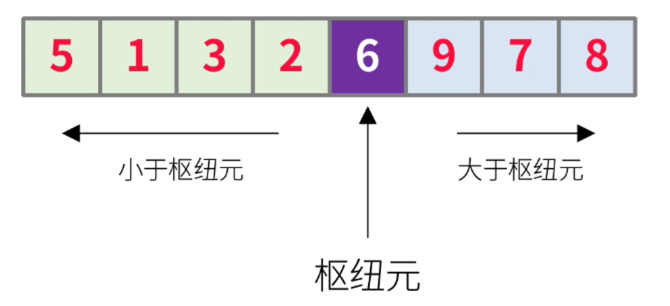
提示
为了便于理解,本例选取数组最右侧的元素作为枢纽元,但是并不代表这种选取方式是最优的。
- 将原数组根据枢纽元划分开来的过程称之为:分区(Partition)
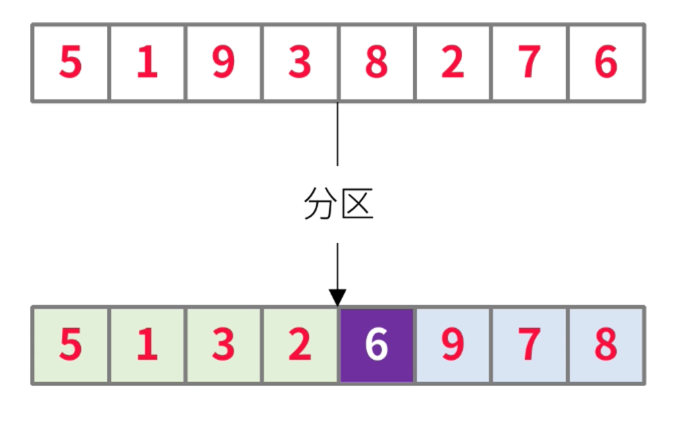
- 第一次分区过程大概是这样的:先确定枢纽元

- 需要再脑海中奖数组的最终目标想象成由下图的几个区域组成

注意:
在分区结束前,枢纽元位置的元素不会发生换位操作
- 为了便于描述,以下将“<=枢纽元”的区域称之为“左侧分区”,将“>枢纽元”的区域称之为“右侧分区”
- 需要再脑海中奖数组的最终目标想象成由下图的几个区域组成
- 使用第一个数字与枢纽元比较大小:
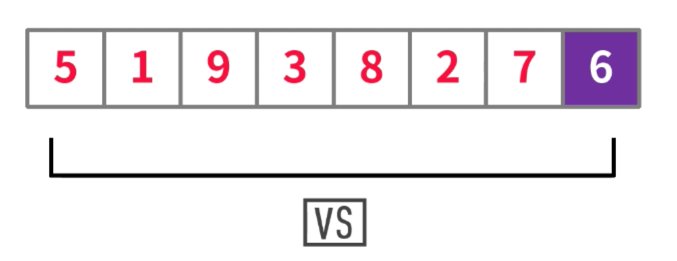
- 由于5小于6,所以,5在左侧分期,并且不用换位

- 再使用数组的第二个元素与枢纽元进行对比
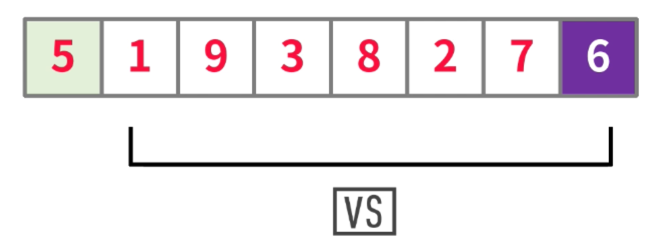
注意:
尽管第二位的1比第一位的5跟小,但不需要换位,后续会使用递归再次处理

- 在使用数组的第三个元素与枢纽元进行对比
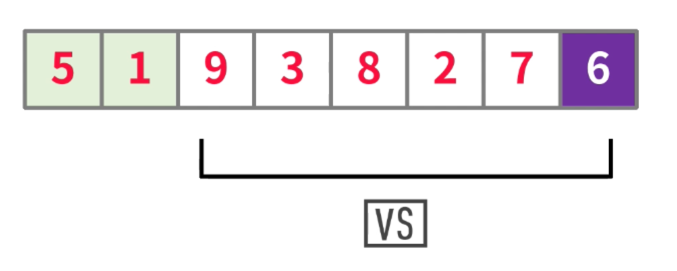
- 由于9大于6,所以,9在右侧区域

注意:
不用换位,只需要标记位置即可,此时枢纽元元素仍在数组的最右侧
- 在使用数组的第四个元素与枢纽元进行对比
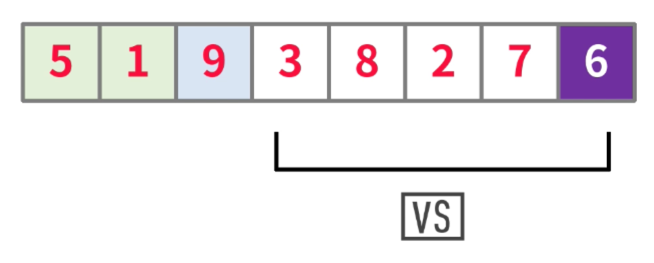
- 由于3小于6,所以,3在左侧的分区
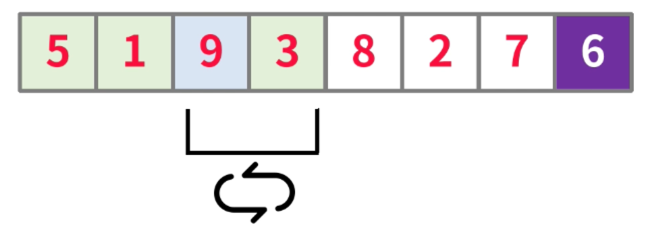
注意:
由于各分区内的元素必须是连续的,所以,此次需要换位
- 后续以此类推,全部完成后,将枢纽元与右侧分区的第一个元素换位
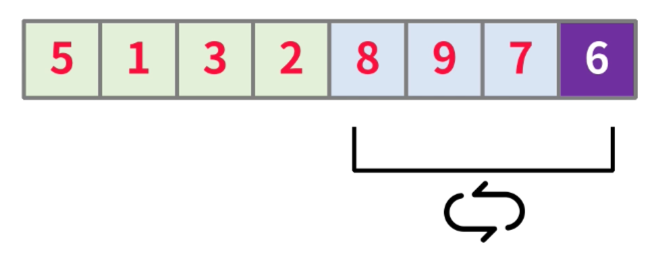
- 得到第一次分区的最终结果

- 接下来,对左右两个分区继续执行相同的操作
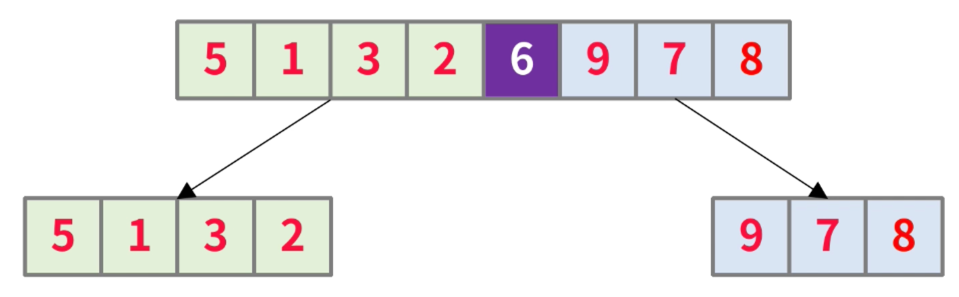
- 最终得到有序的数组(始终对同一个数组的片段进行处理,未拆分,则无需合并)
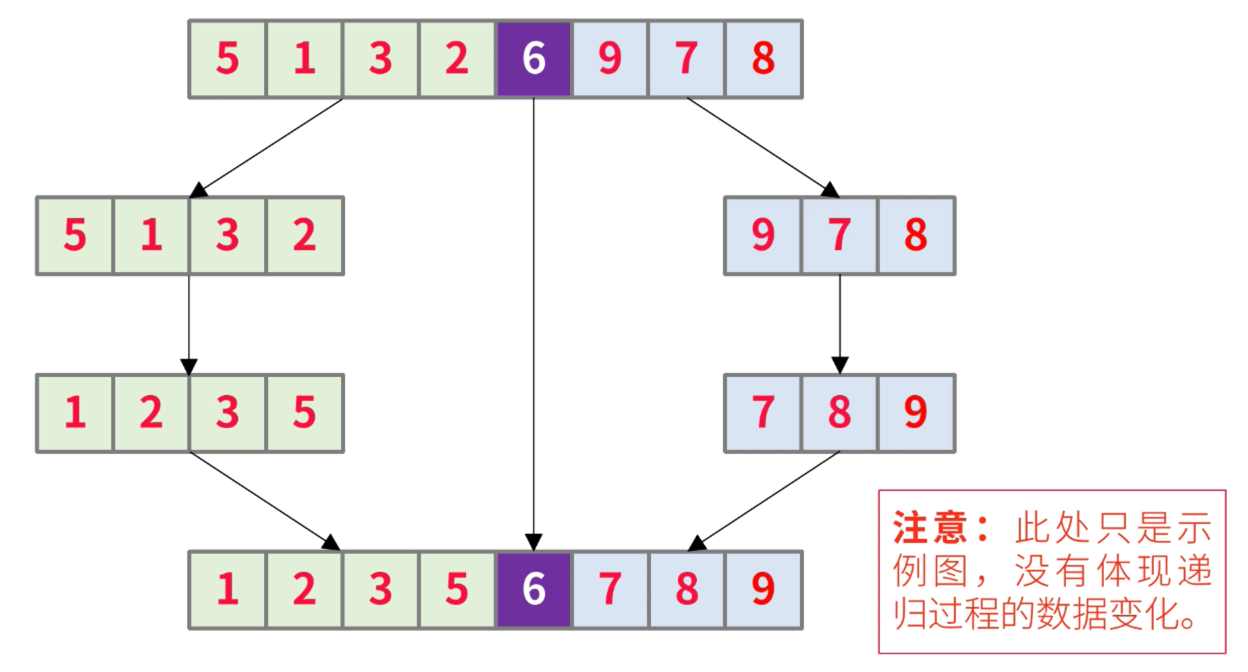
- 第一次分区过程大概是这样的:先确定枢纽元
代码实现
public class QuickSort1 {
public static void main(String[] args) {
int[] array = {8, 1, 4, 9, 0, 3, 5, 2, 7, 6};
System.out.println(Arrays.toString(array));
System.out.println();
quickSort(array, 0, array.length-1);
System.out.println(Arrays.toString(array));
}
/**
* 这是一个自定义的方法
* 注意:快速排序本质上没有拆出新数组,也不需要合并,所以该方法不需要返回值
* @param array 原数组
* @param start 需要被拆分的区间的起始元素下标
* @param end 需要被拆分的区间的结束元素下标
*/
public static void quickSort(int[] array, int start, int end) {
int pivot = array[end];
// 标记左侧区域的位置,在需遍历的数组片段的左侧
int x = start - 1;
// 遍历数组片段
for (int i = start; i < end; i++) {
// 判断当前元素是否小于或等于枢纽元
if (array[i] <= pivot) {
// 判断当前元素的左侧是否已经存在大于枢纽元的元素
if (i - x > 1) {
int tmp = array[i];
array[i] = array[x + 1];
array[x + 1] = tmp;
x++;
} else {
x = i;
}
}
}
// 交换枢纽元与第一个大于枢纽元的元素的位置,即:将枢纽元放在左右区域的中间
if (pivot < array[x + 1]) {
array[end] = array[x + 1];
array[x + 1] = pivot;
}
// 如果左侧区域仍有多个元素,则递归
// 因为x是左侧区域的最右侧元素下标
// 若比需要处理的数组片段的最左侧元素下标大,则表示左侧区域存在超过一个元素
if (x > start) {
quickSort(array, start, x);
}
// 如果右侧区域仍有多个元素,则递归
if (end - x - 1 > 1) {
quickSort(array, x + 2, end);
}
}
}
排序算法的选取
- 在一般情况下,可能比较关注算法所表现出来的运算效率,评估值主要包括:
- 判断次数
- 交换次数
- 耗时
- 可以随机生成50000个随机数构成的数组,并观察以上各指标。
多种排序算法的运算效率
- 50000个随机数的数组排序测试结果参考:
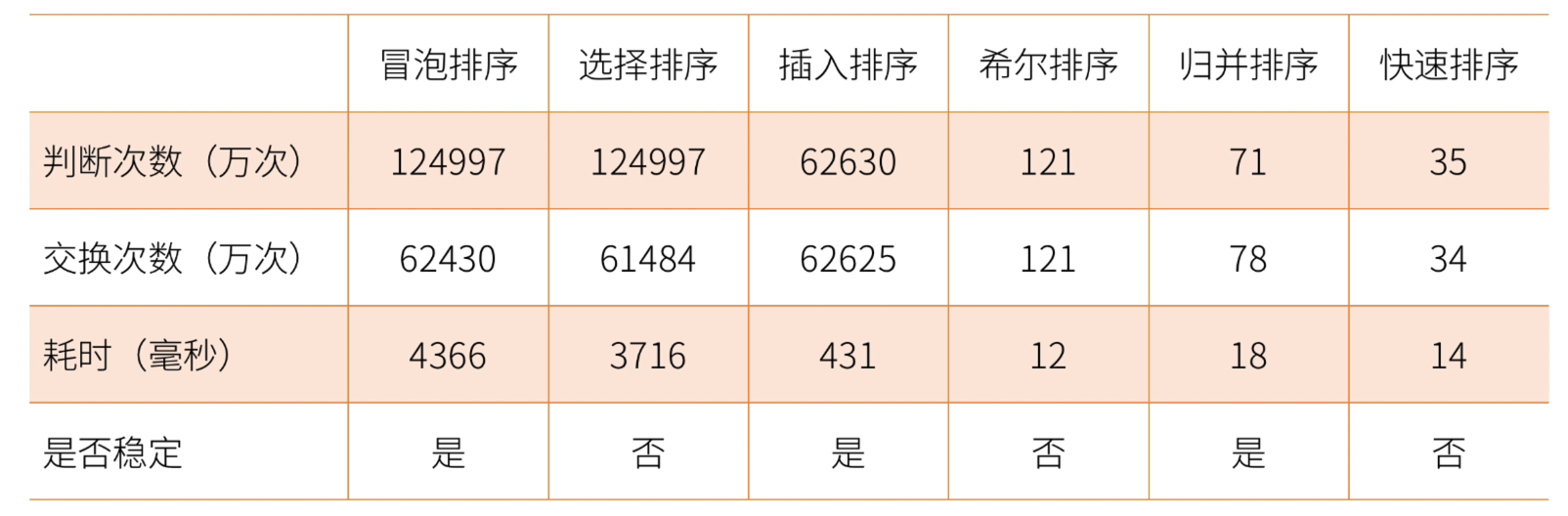
注意
- 一般不建议使用元素特别多的数组,因为有些算法的性能非常差;
- 例如,使用冒泡排序来处理长度为50万的数组,整个排序过程可能需要7分钟以上(仅供参考)
- 由于随机数值大小、初始数组内元素的大小顺序、机器的性能等多方面原因,测试结果仅供参考;
- 例如,在快速排序时,数组元素的顺序直接影响排序效率,另外,插入排序、希尔排序、归并排序也是这样
- 归并排序没有发生实质的交换,而是将原数组的元素有序的填充到新数组,只能使用“填充次数”替代“交换次数”作为参考。
- 另外,还必须关注算法的稳定性
- 算法的稳定性:排序的本质是“交换位置”,在数组中,可能存在多个值完全相同的元素,如果排序前这些元素的位置和排序后一样,则算法是稳定的,如果发生了位置变化,则算法是不稳定的。
- 即使归并排序中没有实质的交换位置,最终结果与原数组对比,也可视为发生了位置的交换。
- 尽管相同值的元素从表面上看是相同的,但是,只要本质上不是同一个,在处理时就应该视为不同的数据
- 例如多本相同的数、同款同型号手机等。。。
- 总的来说,在选取排序算法时,首先要考虑是否关注稳定性,如果需要算法是稳定的,只能在归并排序,插入排序和冒泡排序中选择,并且,有序归并排序的效率最高,应该优先选取归并排序,当然,如果不需要算法是稳定的,快速排序则是最优先考虑的算法。
